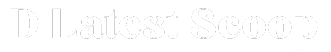Why 538's predictions haven't changed much since the debate

Former President Donald Trump's lead in national polls has widened by just over 2 percentage points since President Joe Biden's weak showing in the first presidential debate of the season on June 27, according to the 538 average. Biden's current lead of 2.1 points is the worst for a Democratic presidential candidate since early 2000, when then-Vice President Al Gore was trailing Texas Gov. George W. Bush by a wide margin, according to the race's retrospective polling average.

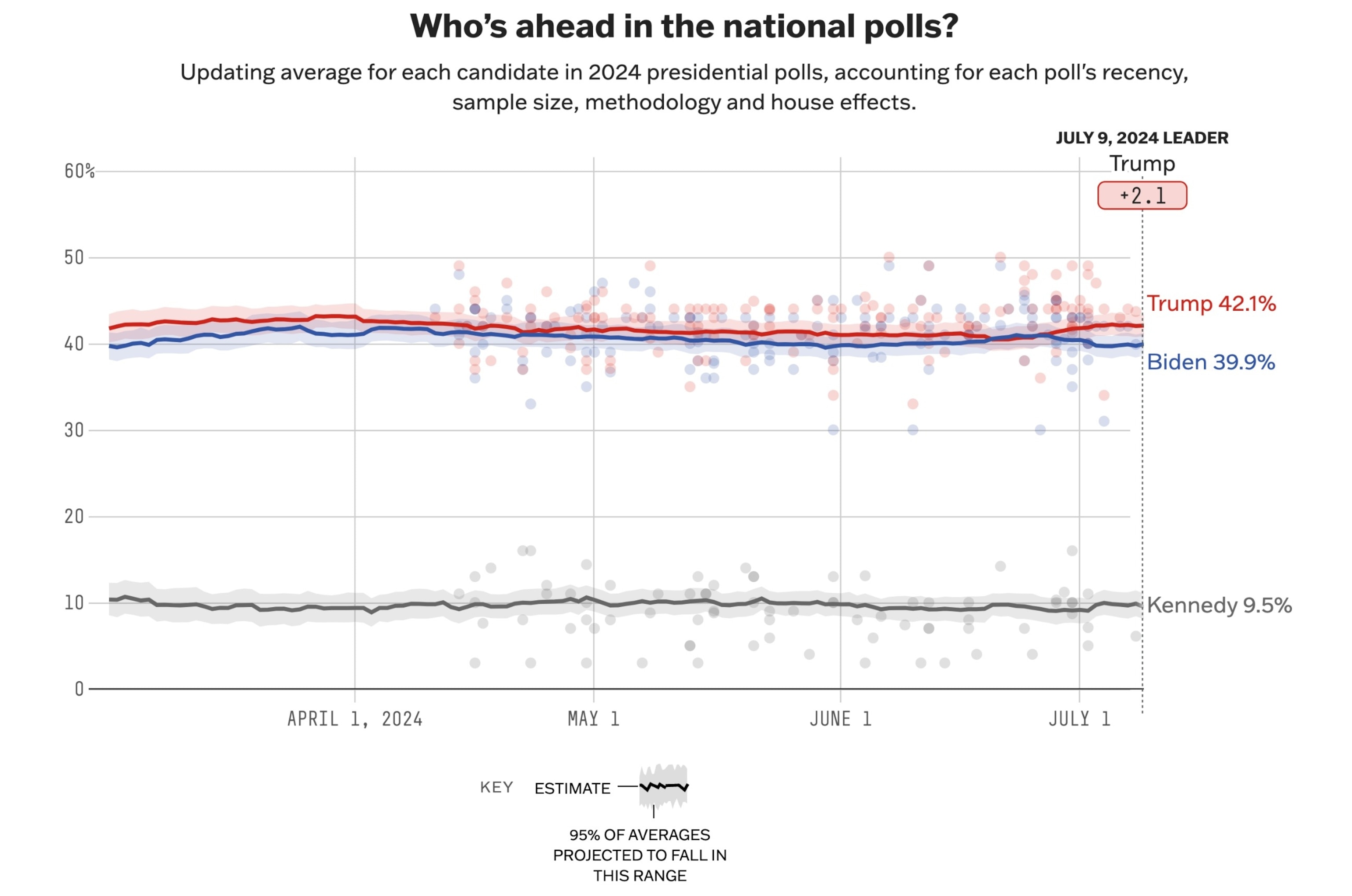
But our projections for the 2024 election have remained largely unchanged. On the day of the debate, we estimated Biden's chances of winning a majority of the electoral votes at 50 in 100. Those chances briefly dropped to 46 in 100 on July 5, but now stand at 48 in 100. At first glance, this lack of movement is puzzling: if Biden has fallen by more than two points from roughly even in the national polls, shouldn't his chances of winning have dropped by more than a few points?

Well, not necessarily. The “right” amount of movement in a forecast depends on how much uncertainty you expect there to be between now and the event you're trying to forecast. For example, it's probably easy to predict how hungry you'll be tomorrow morning; that's a pretty low-volatility prediction (unless you're traveling internationally or running a marathon). But some things are much harder to predict, like medium-term stock returns.

Predicting public opinion four months out is also hard. On the one hand, because small events like debates can lead to big changes in public opinion. But polls themselves are hard to predict because they are noisy. There are lots of sources of uncertainty, and they all need to be combined in the right way. And forecasters make lots of imperfectly informed choices to figure out how to do that (whether they use mental models or the statistical models we use).

To make it easier to understand, let’s break down the main sources of election uncertainty into two parts.

First, there is uncertainty about the accuracy of polls on election day. This is relatively easy to measure. We ran a model to calculate how much polling error has been in recent years and how correlated it was across states. According to the model, if a poll overestimates a Democrat by one point in, say, Wisconsin, the average state is likely to overestimate the Democrat by about 0.8 points. And a state like Michigan, which resembles America’s dairy belt both demographically and politically, is likely to overestimate by nearly 0.9 points. On average, we simulate a poll bias of about 3.5 to 4 points for each scenario in our election model. That is, we would expect the poll to overestimate about 70 percent of the time. which one The difference in support for Democrats or Republicans is expected to be 3.5 points or less, and there is a 95 percent chance that the difference will be less than 8 points.

These are pretty wide uncertainty intervals; about 25% larger than any other election forecasting model I know of. One reason they are so large is because the 538 model more closely tracks trends in the reliability of state-level polls. This is quite simple: polls have been worse recently, so we simulate more of the potential bias between states. We could also make the model take a longer-term view and simulate less of the amount of bias, but such a model would have performed much worse than the current version in 2016 and 2020. Even if the polls are more accurate this year, we would have preferred to have allowed for a scenario in which the polling error is nearly 50% larger than it was in 2020, i.e., 2020 compared to 2016.

But the second, and bigger, source of uncertainty about the election is how much the polls will fluctuate between now and Election Day. By forecasting future changes in the polls, we can effectively “smooth out” the fluctuations in the poll average as we factor them into our Election Day forecasts. Let's think hypothetically for a moment: if a candidate moves up one point in the polls, but we forecast that their polls will move an average of 20 points between now and November, that increase in that candidate's chances of winning will be much less than if we forecast that the polls will move only 10 points.

Today we simulated that the gap between the two candidates in the average state would move by about 8 points on average over the remainder of the election. We got this figure by calculating the daily average of 538 state polls for every election from 1948 to 2020, finding the absolute difference between the poll average on a given day and the average on Election Day, and taking the average of those differences for each day in the election. We found that from 300 days until Election Day to Election Day, the polls move by about 12 points on average. This means that on average, the polls change by about 0.35 points per day.

Admittedly, polls are not as volatile as they used to be—from 2000 to 2020, polls in the average swing state fluctuated by just 8 points, on average, in the 300 days before Election Day—but there are several reasons to use a larger historical dataset rather than subsetting your analysis to recent elections.

First, it is a robust estimate. In election forecasting, we are dealing with very small sample sizes of data and need as many observations as possible. Taking a longer view also better accounts for possible voter realignment, some of which looks likely to occur this year. Given how the race has played out so far, leaving room for volatility may be a safer course of action.

Conversely, simulating low polling error during the election period produces forecasts that assume little poll volatility after Labor Day. This is because the statistical method we use to examine error over time (called a “random walk process”) distributes opinion changes evenly over the election period. However, electoral events that shape voter preferences tend to be concentrated in the fall, toward the end of the election period, and many voters are not paying attention until then. For this reason, we prefer to use a dataset that incorporates larger volatility after Labor Day.

As we can see, both the model errors based on the 1948-2020 elections and the 2000-2020 elections underestimate the actual polling variance that occurred in the final months of those elections. However, underestimating the variance for the 2000-2020 elections is particularly undesirable because it would result in lower errors for more recent elections. Therefore, in our forecasting model, we choose to use a historical dataset that creates more uncertainty early on, and later capture the appropriate amount of uncertainty for more recent elections. However, we still underestimate the variance for some of the oldest elections in our training set. Essentially, the model error we end up using splits the difference between historical polling variance and recent polling variance.

Now it’s time to combine all of this uncertainty. Our model works by updating previous predictions about the election with inferences from polls. In this case, the model starts with a fundamentals-based forecast that uses economic and political factors to predict past state election outcomes. Then the polls are essentially stacked on top of that forecast. The model’s cumulative forecast is weighted more heavily to the predictions it is more certain about, either the fundamentals-based forecast based on history or a forecast of what the polls will be on Election Day and whether they will be accurate. At this point, we’re less certain about what the polls will show in November, and so the weight our final forecast places on today’s polls is reduced.

In other words, the reason our projections haven't changed much since the debates is because a 2-point change in the race today doesn't necessarily translate into a 2-point change on Election Day. The only way to take the polls more seriously is to just wait.

Just for fun, let's see what the predictions look like with different model settings. I ran the model four times: once as is (error rate of 8 points), once with a moderate poll movement (about 6 points between now and November), once with relatively little movement (4 points), and finally a version with very little poll movement and no consideration of past fundamentals (a purely poll-only model).

The results from these different model settings show that the less uncertainty there is about how the race will play out, the more likely a Trump victory is. This is because Trump is leading in the polls today. So, as we move the poll projections on Election Day closer to where we are today, Biden's margin of victory drops, moving him further away from the fundamentals and closer to the outcome if the election were held today. And if we remove the fundamentals from the model entirely, a Trump victory becomes even more likely.

And this is why the 538 prediction is more stable than the other predictions, most of which take the current polls more seriously. It's not necessarily a wrong prediction. About the future; I found that backtesting doesn't work well if there are few errors. HistoricallyVarious statistical models can help somewhat in explaining electoral uncertainty, but with so few historical examples it is impossible to say which is right or which is wrong.